Непрерывные дроби. Значение непрерывные дроби в словаре кольера. Разложение в цепную дробь
Рассмотрим последовательность
А что будет получаться при дальнейшем возрастании n? Существует ли предел Чему может равняться этот предел?
Рассмотрим положительное число х, определяемое как предел выражения

Перенесем единицу влево:

Это равенство равносильно такому:

откуда (х-1 (2+x-1) = 1 и, следовательно, ![]() или
или

Выражение в правой части называется цепной или непрерывной дробью. В общем виде ее можно записать так:

где а, b, с, d, вообще говоря, различные целые числа.
Если, начиная с некоторого места, повторяются одинаковые числа (или одинаковые конечные последовательности чисел), то непрерывная дробь называется периодической . Выше показано, что число может быть записано в виде периодической непрерывной дроби, хотя, как известно, это число, как и всякое другое иррациональное число, невозможно записать в виде десятичной периодической дроби .
Если десятичную периодическую дробь оборвать на каком-либо месте, мы получим ее приближенное значение (с недостатком). Например:
Оборвав непрерывную дробь, мы тоже получим ее приближенное значение в виде рационального числа. Мы видели, что и т. д. Эти дроби называют подходящими дробями для данной непрерывной дроби; в самом деле, каждая следующая подходящая дробь все ближе подходит к предельному значению данной дроби, или, иначе, дает все более точное приближение этого значения.
Можно доказать, что подходящие дроби четного порядка всегда меньше их предельного значения, а подходящие дроби нечетного порядка больше их предельного значения. Например, нетрудно проверить, что

В статье "О непрерывных дробях" (1737) Эйлер впервые указал приемы преобразования таких дробей и показал связь непрерывных периодических дробей с квадратными уравнениями и квадратическими иррациональностями. Там же показано выражение основания натуральных логарифмов, числа е * (е = 2,71828182845...), с помощью непериодической непрерывной дроби

* (Число е можно определить как  . Оно играет, как и число π, важную роль в анализе и его приложениях.
)
. Оно играет, как и число π, важную роль в анализе и его приложениях.
)
Вот еще некоторые простые разложения в непрерывные дроби, найденные Эйлером:

Разлагая в бесконечную цепную дробь е и е 2 , Эйлер, по существу, доказал иррациональность этих чисел, т. е. невозможность равенств ![]() , где m, n, р, q - произвольные натуральные числа.
, где m, n, р, q - произвольные натуральные числа.
Пользуясь этим, И. Г. Ламберт несколько лет спустя получил представление некоторых функций в форме бесконечных непрерывных дробей, например
Цепные дроби были введены в 1572 году итальянским математиком Бомбелли. Современное обозначение непрерывных дробей встречается у итальянского математика Катальди в 1613 году. Величайший математик XVIII века Леонардо Эйлер первый изложил теорию цепных дробей, поставил вопрос об их использовании для решения дифференциальных уравнений, применил их к разложению функций, представлению бесконечных произведений, дал важное их обобщение.
Работы Эйлера по теории цепных дробей были продолжены М. Софроновым (1729-1760), академиком В.М. Висковатым (1779-1819), Д. Бернулли (1700-1782) и др. Многие важные результаты этой теории принадлежат французскому математику Лагранжу, который нашел метод приближенного решения с помощью цепных дробей дифференциальных уравнений.
Алгоритм Евклида дает возможность найти представление (или разложение) любого рационального числа в виде цепной дроби. В качестве элементов цепной дроби получаются неполные частные последовательных делений в системе равенств (1), поэтому элементы цепной дроби называются также неполными частными. Кроме того, равенства системы (2) показывают, что процесс разложения в цепную дробь состоит в последовательном выделении целой части и перевертывании дробной части.
Последняя точка зрения является более общей по сравнению с первой, так как она применима к разложению в непрерывную дробь не только рационального, но и любого действительного числа.
Разложение рационального числа имеет, очевидно, конечное число элементов, так как алгоритм Евклида последовательного деления a на b является конечным.
Понятно, что каждая цепная дробь представляет определенное рациональное число, то есть равна определенному рациональному числу. Но возникает вопрос, не имеются ли различные представления одного и того же рационального числа цепной дробью? Оказывается, что не имеются, если потребовать, чтобы было.
Непрерывные дроби - последовательность, каждый член которой является обычной дробью, порождает непрерывную (или цепную) дробь, если ее второй член прибавить к первому, а каждую дробь, начиная с третьей, прибавить к знаменателю предыдущей дроби. Например, последовательность 1, 1/2, 2/3, 3/4, ..., n/(n + 1), ... порождает непрерывную дробь где многоточие в конце указывает на то, что процесс продолжается бесконечно. В свою очередь непрерывная дробь порождает другую последовательность дробей, называемых подходящими. В нашем примере первая, вторая, третья и четвертая подходящие дроби равны и Их можно построить по простому правилу из последовательности неполных частных 1, 1/2, 2/3, 3/4, ... Прежде всего выпишем первую и вторую подходящие дроби 1/1 и 3/2. Третья подходящая дробь равна (2?1 + 3?3)/(2?1 + 3?2) или 11/8, ее числитель равен сумме произведений числителей первой и второй подходящих дробей, умноженных соответственно на числитель и знаменатель третьего неполного частного, а знаменатель равен сумме произведений знаменателей первого и второго неполных частных, умноженных соответственно на числитель и знаменатель третьего неполного частного. Четвертая подходящая дробь получается аналогично из четвертого неполного частного 3/4 и второй и третьей подходящих дробей: (3?3 + 4?11)/(3?2 + 4?8) или 53/38. Следуя этому правилу, находим первые семь подходящих дробей: 1/1, 3/2, 11/8, 53/38, 309/222, 2119/1522 и 16687/11986. Запишем их в виде десятичных дробей (с шестью знаками после запятой): 1,000000; 1,500000; 1,375000; 1,397368; 1,391892; 1,392247 и 1,392208. Значением нашей непрерывной дроби будет число x, первые цифры которого 1,3922. Подходящие дроби являются лучшим приближением числа x. Причем они поочередно оказываются то меньше, то больше числа x (нечетные - больше x, а четные - меньше). Чтобы представить отношение двух положительных целых чисел в виде конечной непрерывной дроби, нужно воспользоваться методом нахождения наибольшего общего делителя. Например, возьмем отношение 50/11. Так как 50 = 4?11 + 6 или 11/50 = 1/(4 + 6/11), и, аналогично, 6/11 = 1/(1 + 5/6) или 5/6 = 1/(1 + 1/5), получаем: Непрерывные дроби используются для приближения иррациональных чисел к рациональным. Предположим, что x - иррациональное число (т.е. непредставимо в виде отношения двух целых чисел). Тогда, если n0 - наибольшее целое число, которое меньше x, то x = n0 + (x - n0), где x - n0 - положительное число меньше 1, поэтому обратное ему число x1 больше 1 и x = n0 + 1/x1. Если n1 - наибольшее целое число, которое меньше x1, то x1 = n1 + (x1 - n1), где x1 - n1 - положительное число, которое меньше 1, поэтому обратное ему число x2 больше 1, и x1 = n1 + 1/x2. Если n2 - наибольшее целое число, которое меньше x2, то x2 = n2 + 1/x3, где x3 больше 1, и т.д. В результате мы шаг за шагом находим последовательность неполных частных n0, 1/n1, 1/n2, ... непрерывной дроби, являющихся приближениями x. Поясним сказанное на примере. Предположим, что тогда первые 6 подходящих дробей равны 1/1, 3/2, 7/5, 17/12, 41/29, 99/70. Записанные в виде десятичных дробей они дают следующие приближенные значения: 1,000; 1,500; 1,400; 1,417; 1,4137; 1,41428. Непрерывная дробь имеет неполные частные 1, 1/1, 1/2, 1/1, 1/2, 1/1, .... Иррациональное число является корнем квадратного уравнения с целочисленными коэффициентами в том и только в том случае, если неполные частные его разложения в непрерывную дробь периодичны. Непрерывные дроби тесно связны со многими разделами математики, например с теорией функций, расходящимися рядами, проблемой моментов, дифференциальными уравнениями и бесконечными матрицами. Если x - радианная мера острого угла, то тангенс угла x равен значению непрерывной дроби с неполными частными 0, x/1, ?x2/3, ?x2/7, ?x2/9, ..., а если x - положительное число, то натуральный логарифм от 1 + x равен значению непрерывной дроби с неполными частными 0, x/1, 12x/2, 12x/3, 22x/4, 22x/5, 32x/6, …. Формальным решением дифференциального уравнения x2dy/dx + y = 1 + x в виде степенного ряда является расходящийся степенной ряд 1 + x - 1!x2 + 2!x3 - 3!x4 + ... . Этот степенной ряд можно преобразовать в непрерывную дробь с неполными частными 1, x/1, x/1, 2x/1, 2x/1, 3x/1, 3x/1, ..., а ее в свою очередь использовать для получения решения дифференциального уравнения x2dy/dx + y = 1 + x.
План:
-
Введение
- 1 Разложение в цепную дробь
- 2 Подходящие дроби
- 3
Приближение вещественных чисел рациональными
- 3.1 Примеры
- 4 Свойства и примеры
- 5
Приложения цепных дробей
- 5.1 Теория календаря
- 5.2 Решение сравнений первой степени
- 5.3
Другие приложения
- 5.3.1 Свойства золотого сечения
- 6 Историческая справка
- 7 Мотивация Примечания
Введение
Цепная дробь (или непрерывная дробь ) - это математическое выражение вида
где a 0 есть целое число и все остальные a n натуральные числа (то есть неотрицательные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или бесконечной). Число представляется конечной цепной дробью тогда и только тогда, когда оно рационально. Число представляется периодической цепной дробью тогда и только тогда, когда оно является квадратичной иррациональностью.
1. Разложение в цепную дробь
Любое вещественное число x может быть представлено (конечной или бесконечной) цепной дробью , где
где обозначает целую часть числа x .
Для рационального числа x это разложение оборвётся по достижении нулевого x n для некоторого n. В этом случае x представляется конечной цепной дробью .
Для иррационального x все величины x n будут ненулевыми и процесс разложения можно продолжать бесконечно. В этом случае x представляется бесконечной цепной дробью .
Для рациональных чисел может быть использован алгоритм Евклида для быстрого получения разложения в цепную дробь.
2. Подходящие дроби
n -ой подходящей дробью для цепной дроби , называется конечная цепная дробь , значение которой равно некоторому рациональному числу . Подходящие дроби с чётными номерами образуют возрастающую последовательность, предел которой равен x . Аналогично, подходящие дроби с нечётными номерами образуют убывающую последовательность, предел которой также равен x .
Эйлер вывел рекуррентные формулы для вычисления числителей и знаменателей подходящих дробей:
Таким образом, величины p n и q n представляются значениями континуант:
Последовательности и являются возрастающими.
Числители и знаменатели соседних подходящих дробей связаны соотношением:
| p n q n - 1 - q n p n - 1 = (- 1) n - 1 , | (1) |
которое можно переписать в виде
Откуда следует, что
3. Приближение вещественных чисел рациональными
Цепные дроби позволяют эффективно находить хорошие рациональные приближения вещественных чисел. А именно, если вещественное число x разложить в цепную дробь, то её подходящие дроби будут удовлетворять неравенству
Отсюда, в частности, следует:
3.1. Примеры
- Разложим число π =3,14159265… в непрерывную дробь и подсчитаем его подходящие дроби: 3, 22/7, 333/106, 355/113, 103993/33102, …
4. Свойства и примеры
- Любое рациональное число может быть представлено в виде конечной цепной дроби двумя способами, например:
- Теорема Лагранжа : Число представляется в виде бесконечной периодической цепной дроби тогда и только тогда, когда оно является иррациональным решением квадратного уравнения с целыми коэффициентами.
для числа
- У числа пи простой закономерности не видно:
- Теорема Гаусса - Кузьмина: Почти для всех (кроме множества меры нуль) вещественных чисел существует среднее геометрическое коэффициентов соответствующих им цепных дробей, и оно равно постоянной Хинчина.
- Теорема Маршалла Холла. Если в разложении числа x в непрерывную дробь, начиная со второго элемента не встречаются числа большие n , то говорят, что число x относится к классу F (n ). Любое вещественное число может быть представленно в виде суммы двух чисел из класса F (4) и в виде произведения двух чисел из класса F (4). В дальнейшем было показано, что любое вещественное число может быть представленно в виде суммы 3 чисел из класса F (3) и в виде суммы 4 чисел из класса F (2). Количество требуемых слагаемых в этой теореме не может быть уменьшено - для представления некоторых чисел указанным образом меньшего количества слагаемых недостаточно.
5. Приложения цепных дробей
5.1. Теория календаря
При разработке солнечного календаря необходимо найти рациональное приближение для числа дней в году, которое равно 365,2421988… Подсчитаем подходящие дроби для дробной части этого числа:
Первая дробь означает, что раз в 4 года надо добавлять лишний день; этот принцип лёг в основу юлианского календаря. При этом ошибка в 1 день накапливается за 128 лет. Второе значение (7/29) никогда не использовалось. Третья дробь (8/33), то есть 8 високосных лет за период в 33 года, была предложена Омаром Хайямом в XI веке и положила начало персидскому календарю, в котором ошибка в день накапливается за 4500 лет (в григорианском - за 3280 лет). Очень точный вариант с четвёртой дробью (31/128, ошибка в сутки накапливается только за 100000 лет) пропагандировал немецкий астроном Иоганн фон Медлер (1864), однако большого интереса он не вызвал.
5.2. Решение сравнений первой степени
Рассмотрим сравнение: , где известны, причём можно считать, что a взаимно просто с m . Надо найти x .
Разложим в непрерывную дробь. Она будет конечной, и последняя подходящая дробь . Подставим в формулу (1):
m q n − 1 − a p n − 1 = (− 1) n − 1Отсюда вытекает:
, или:Вывод: класс вычетов является решением исходного сравнения.
5.3. Другие приложения
5.3.1. Свойства золотого сечения
Интересный результат, которые следует из того факта, что выражение непрерывной дроби для φ не использует целых чисел больше чем 1, состоит в том, что φ является одним из самых "трудных" действительных чисел для приближения с помощью рациональных чисел. Одна теорема (Теорема Гурвица) утверждает, что любое действительное число k может быть приближено дробью m /n при помощи
Тогда когда практически все действительные числа k имеют в конечно счёте бесконечно много приближений m /n , которые находятся на значительно меньшем расстояние от k , чем этот предел, приближения для φ (т.е. числа 5/3, 8/5, 13/8, 21/13, и т.д.) последовательно "касаются границы", удерживая расстояние на почти точно расстоянии от φ, тем самым никогда не создавая приближения столь же внушительные как, к примеру, 355/113 для π. Может быть показано что любое действительное число формы (a + b φ)/(c + d φ) – где a , b , c иd являются целыми числами, такими как ad − bc = ±1 – имеют такое же свойство как и золотое сечение φ; а также, что все остальные действительные числа могут быть приближены намного лучше.
6. Историческая справка
Античные математики умели представлять отношения несоизмеримых величин в виде цепочки последовательных подходящих отношений, получая эту цепочку с помощью алгоритма Евклида. По-видимому, именно таким путём Архимед получил приближение - это 12-я подходящая дробь для или от 4-й подходящей дроби для .
В V веке индийский математик Ариабхата применял аналогичный «метод измельчения» для решения неопределённых уравнений первой и второй степени. С помощью этой же техники было, вероятно, получено известное приближение для числа π (355/113). В XVI веке Рафаэль Бомбелли извлекал с помощью цепных дробей квадратные корни (см. его алгоритм).
Начало современной теории цепных дробей положил в 1613 году Пьетро Антонио Катальди. Он отметил основное их свойство (положение между подходящими дробями) и ввёл обозначение, напоминающее современное. Позднее его теорию расширил Джон Валлис, который и предложил термин «непрерывная дробь» . Эквивалентный термин «цепная дробь » появился в конце XVIII века.
Применялись эти дроби в первую очередь для рационального приближения вещественных чисел; например, Христиан Гюйгенс использовал их для проектирования зубчатых колёс своего планетария. Гюйгенс уже знал, что подходящие дроби всегда несократимы и что они представляют наилучшее рациональное приближение.
В XVIII веке теорию цепных дробей в общих чертах завершили Леонард Эйлер и Жозеф Луи Лагранж.
7. Мотивация
Непрерывные дроби являются самыми "математически естественными" представлениями вещественных чисел.
Большинство людей знакомы с десятичным представлением вещественных чисел, которое может быть определено как
где a 0 может быть любым целым числом, а последующие a i являются одним из элементом {0,1,2,…,9}. В этом представление, число π, к примеру, может быть представлено как последовательность целых чисел .
Это десятичное представление имеет несколько проблем. Одна из них, многие рациональные числа не имеет конечного представления в этой системе. Например, число 1/3 представимо бесконечной последовательностью (0,3,3,3,3,…). Другая проблема заключается в том, что константа 10 является по сути произвольным выбором, который оказывает предпочтение числам, которые как-либо относятся к целому числу 10. Например, 137/1600 имеет конечное десятичное представление, тогда как 1/3 не имеет, не потому, что 137/1600 проще чем 1/3, а всего лишь потому, что 1600 делит степень 10 (10 6 = 1600 × 625). Запись как цепная дробь является представлением вещественных чисел, которая не имеет этих проблем.
Давайте рассмотрим как мы можем описать число, такое как 415/93, которое примерно равняется 4,4624. Это примерно 4.Вообще-то это чуть больше чем 4, около 4 + 1/2. Но 2 в знаменателе не совсем точно; там должно быть число чуть больше чем 2, примерно 2 + 1/6. Таким образом, 415/93 примерно равняется 4 + 1/(2 + 1/6). Но 6 в знаменателе не верно; настоящее значение чуть больше 6, 6+1/7. Таким образом, 415/93 является 4+1/(2+1/(6+1/7). Это точное значение.
Опуская некоторые обязательные части в выражении 4 + 1 / (2 + 1 / (6 + 1 / 7)) мы получим краткую нотацию . (Заметьте, что общепринято заменять только первую запятую точкой с запятой).
Представление как непрерывная дробь вещественного числа может быть определена таким образом. Она имеет несколько желательных свойств:
- Представление как непрерывная дробь конечно тогда и только тогда когда число является рациональным.
- Каждое рациональное число имеет по-существу единственное представление как непрерывная дробь. Каждое рациональное число можно представить в точности двумя способами, т.к. [a 0 ; a 1 , … a n − 1 , a n ] = [a 0 ; a 1 , … a n − 1 , a n − 1, 1]. Математики предпочитают иметь взаимно-однозначное соответствие между рациональными числами и цепными дробями; первая, более короткая нотация выбрана в качество каноническое представления.
- Представление как непрерывная дробь иррационального числа единственно.
- Цепная дробь является периодической тогда и только тогда, когда число является квадратичной иррациональностью, т.е. имеет форму
для целых a , b , c , d ; где b и d не ноль и c >1 и c не является точным квадратом.
К примеру, периодическая непрерывная дробь является золотым сечением, а периодическая непрерывная дробь является квадратным корнем из 2.
- Раннее усечение представления числа x в виде цепной дроби приводит к рациональному приближению x, которая в определенном смысле является "наилучшим" рациональным приближением.
Последнее свойство чрезвычайно важно. У десятичного представления числа его нет. Усечение десятичного представления числа приводит к рациональному приближению числа, но обычно к не очень хорошему приближению. К примеру, усечение 1/7 = 0.142857… в разных местах приводит к приближениям таким как 142/1000, 14/100 и 1/10. Но очевидно лучшим рациональным приближением будет само число "1/7". Обрывая десятичное представление π мы получаем приближения такие как 31415/10000 и 314/100. Цепная дробь π начинается . Усекая это представление мы получаем отличные рациональные приближение 3, 22/7, 333/106, 355/113, 103993/33102, …. Знаменатели 314/100 и 333/106 почти одинаковые, но ошибка в приближении 314/100 в девятнадцать раз больше ошибки, чем в приближении 333/106. Как приближении π, более чем в сто раз точнее приближения 3,1416.
, Дробь , Дробь (математика) , Правильная дробь .НЕПРЕРЫВНЫЕ ДРОБИ. Последовательность, каждый член которой является обычной дробью, порождает непрерывную (или цепную) дробь, если ее второй член прибавить к первому, а каждую дробь, начиная с третьей, прибавить к знаменателю предыдущей дроби.
Например, последовательность 1, 1/2, 2/3, 3/4,..., n /(n + 1),... порождает непрерывную дробь
где многоточие в конце указывает на то, что процесс продолжается бесконечно. В свою очередь непрерывная дробь порождает другую последовательность дробей, называемых подходящими. В нашем примере первая, вторая, третья и четвертая подходящие дроби равны
Их можно построить по простому правилу из последовательности неполных частных 1, 1/2, 2/3, 3/4,.... Прежде всего выпишем первую и вторую подходящие дроби 1/1 и 3/2. Третья подходящая дробь равна (2Ч 1 + 3Ч 3)/(2Ч 1 + 3Ч 2) или 11/8, ее числитель равен сумме произведений числителей первой и второй подходящих дробей, умноженных соответственно на числитель и знаменатель третьего неполного частного, а знаменатель равен сумме произведений знаменателей первого и второго неполных частных, умноженных соответственно на числитель и знаменатель третьего неполного частного. Четвертая подходящая дробь получается аналогично из четвертого неполного частного 3/4 и второй и третьей подходящих дробей: (3Ч 3 + 4Ч 11)/(3Ч 2 + 4Ч 8) или 53/38. Следуя этому правилу, находим первые семь подходящих дробей: 1/1, 3/2, 11/8, 53/38, 309/222, 2119/1522 и 16687/11986. Запишем их в виде десятичных дробей (с шестью знаками после запятой): 1,000000; 1,500000; 1,375000; 1,397368; 1,391892; 1,392247 и 1,392208. Значением нашей непрерывной дроби будет число x , первые цифры которого 1,3922. Подходящие дроби являются лучшим приближением числа x . Причем они поочередно оказываются то меньше, то больше числа x (нечетные – больше x , а четные – меньше).
Чтобы представить отношение двух положительных целых чисел в виде конечной непрерывной дроби, нужно воспользоваться методом нахождения наибольшего общего делителя. Например, возьмем отношение 50/11. Так как 50 = 4Ч 11 + 6 или 11/50 = 1/(4 + 6/11), и, аналогично, 6/11 = 1/(1 + 5/6) или 5/6 = 1/(1 + 1/5), получаем:
Непрерывные дроби используются для приближения иррациональных чисел рациональными. Предположим, что x – иррациональное число (т.е. непредставимо в виде отношения двух целых чисел). Тогда, если n 0 – наибольшее целое число, которое меньше x , то x = n 0 + (x – n 0), где x – n 0 – положительное число меньше 1, поэтому обратное ему число x 1 больше 1 и x = n 0 + 1/x 1 . Если n 1 – наибольшее целое число, которое меньше x 1 , то x 1 = n 1 + (x 1 – n 1), где x 1 – n 1 – положительное число, которое меньше 1, поэтому обратное ему число x 2 больше 1, и x 1 = n 1 + 1/x 2 . Если n 2 – наибольшее целое число, которое меньше x 2 , то x 2 = n 2 + 1/x 3 , где x 3 больше 1, и т.д. В результате мы шаг за шагом находим последовательность неполных частных n 0 , 1/n 1 , 1/n 2 ,... непрерывной дроби, являющихся приближениями x .
Поясним сказанное на примере. Предположим, что , тогда
Первые 6 подходящих дробей равны 1/1, 3/2, 7/5, 17/12, 41/29, 99/70. Записанные в виде десятичных дробей они дают следующие приближенные значения : 1,000; 1,500; 1,400; 1,417; 1,4137; 1,41428. Непрерывная дробь для имеет неполные частные 1, 1/1, 1/2, 1/1, 1/2, 1/1,.... Иррациональное число является корнем квадратного уравнения с целочисленными коэффициентами в том и только в том случае, если неполные частные его разложения в непрерывную дробь периодичны.
Непрерывные дроби тесно связны со многими разделами математики, например с теорией функций, расходящимися рядами, проблемой моментов, дифференциальными уравнениями и бесконечными матрицами. Если x – радианная мера острого угла, то тангенс угла x x /1, - x 2 /3, - x 2 /7, - x 2 /9, ..., а если x – положительное число, то натуральный логарифм от 1 + x равен значению непрерывной дроби с неполными частными 0, x /1, 1 2 x /2, 1 2 x /3, 2 2 x /4, 2 2 x /5, 3 2 x /6,... . Формальным решением дифференциального уравнения x 2 dy /dx + y = 1 + x в виде степенного ряда является расходящийся степенной ряд 1 + x – 1!x 2 + 2!x 3 – 3!x 4 +.... Этот степенной ряд можно преобразовать в непрерывную дробь с неполными частными 1, x /1, x /1, 2x /1, 2x /1, 3x /1, 3x /1,..., а ее в свою очередь использовать для получения решения дифференциального уравнения x 2 dy /dx + y = 1 + x .
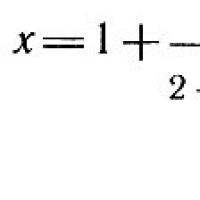 Значение непрерывные дроби в словаре кольера
Значение непрерывные дроби в словаре кольера Генрих Мореплаватель. Биография. Открытия. Биография генриха мореплавателя Энрике мореплаватель что открыл
Генрих Мореплаватель. Биография. Открытия. Биография генриха мореплавателя Энрике мореплаватель что открыл Какое имеет значение мантра «Ом мани падме хум»
Какое имеет значение мантра «Ом мани падме хум» Постные голубцы с гречкой и грибами
Постные голубцы с гречкой и грибами Правдивое онлайн-гадание стрела судьбы
Правдивое онлайн-гадание стрела судьбы Когда ближайшее полнолуние в декабре
Когда ближайшее полнолуние в декабре