Основна механика за манекени. Въведение. Теоретична механика за инженери и изследователи Основни формули на термех
Кинематика
Кинематика на материална точка
Определяне на скоростта и ускорението на точка чрез дадените уравнения на нейното движение
Дадено е: Уравнения на движение на точка: x = 12 sin(πt/6), см; y= 6 cos 2 (πt/6), см.
Задайте вида на неговата траектория за момента t = 1 секнамерете положението на точката върху траекторията, нейната скорост, общо, тангенциално и нормално ускорение, както и радиуса на кривината на траекторията.
Постъпателно и въртеливо движение на твърдо тяло

дадени:
t = 2 s; r 1 = 2 cm, R 1 = 4 cm; r 2 = 6 cm, R 2 = 8 cm; r 3 = 12 cm, R 3 = 16 cm; s 5 = t 3 - 6t (cm).
Определете в момент t = 2 скоростите на точките A, C; ъглово ускорение на колело 3; ускорение на точка B и ускорение на стелаж 4.
Кинематичен анализ на плосък механизъм

дадени:
R 1, R 2, L, AB, ω 1.
Намерете: ω 2.

Плоският механизъм се състои от пръти 1, 2, 3, 4 и плъзгач E. Прътите са свързани с помощта на цилиндрични панти. Точка D се намира в средата на пръта AB.
Дадено е: ω 1, ε 1.
Намерете: скорости V A, V B, V D и V E; ъглови скорости ω 2, ω 3 и ω 4; ускорение a B ; ъглово ускорение ε AB на връзка AB; позиции на центровете за моментна скорост P 2 и P 3 на връзки 2 и 3 на механизма.
Определяне на абсолютна скорост и абсолютно ускорение на точка

Правоъгълна плоча се върти около фиксирана ос по закона φ = 6 t 2 - 3 t 3. Положителната посока на ъгъла φ е показана на фигурите с дъгообразна стрелка. Ос на въртене OO 1 лежи в равнината на плочата (плочата се върти в пространството).
Точка M се движи по плочата по правата BD. Даден е законът за относителното му движение, т.е. зависимостта s = AM = 40 (t - 2 t 3) - 40(s - в сантиметри, t - в секунди). Разстояние b = 20 см. На фигурата точка M е показана в позиция, където s = AM > 0 (при с< 0 точка М е от другата страна на точка А).
Намерете абсолютната скорост и абсолютното ускорение на точка M в момент t 1 = 1 s.
Динамика
Интегриране на диференциални уравнения на движение на материална точка под въздействието на променливи сили
Товар D с маса m, получил начална скорост V 0 в точка А, се движи в извита тръба ABC, разположена в вертикална равнина. В участък AB, чиято дължина е l, товарът се действа от постоянна сила T (посоката му е показана на фигурата) и сила R на средното съпротивление (модулът на тази сила R = μV 2, векторът R е насочен противоположно на скоростта V на товара).
Товарът, завършил движението си в участък AB, в точка B на тръбата, без да променя стойността на скоростния си модул, се придвижва в участък BC. В участък BC товарът се въздейства от променлива сила F, чиято проекция F x върху оста x е дадена.
Считайки товара за материална точка, намерете закона за неговото движение в сечение BC, т.е. x = f(t), където x = BD. Пренебрегнете триенето на товара върху тръбата.

Изтеглете решението на проблема
Теорема за промяната на кинетичната енергия на механична система
Механичната система се състои от тежести 1 и 2, цилиндрична ролка 3, двустепенни макари 4 и 5. Телата на системата са свързани с резби, навити на макарите; секциите на нишките са успоредни на съответните равнини. Ролката (твърд хомогенен цилиндър) се търкаля по опорната равнина без плъзгане. Радиусите на стъпалата на макарите 4 и 5 са съответно равни на R 4 = 0,3 m, r 4 = 0,1 m, R 5 = 0,2 m, r 5 = 0,1 m. Масата на всяка макара се счита за равномерно разпределена външния му ръб. Опорните равнини на товари 1 и 2 са грапави, коефициентът на триене при плъзгане за всеки товар е f = 0,1.
Под действието на сила F, чийто модул се променя по закона F = F(s), където s е преместването на точката на нейното приложение, системата започва да се движи от състояние на покой. Когато системата се движи, върху макарата 5 действат съпротивителни сили, чийто момент спрямо оста на въртене е постоянен и равен на M 5 .
Определете стойността на ъгловата скорост на макарата 4 в момента, когато преместването s на точката на прилагане на сила F стане равно на s 1 = 1,2 m. 
Изтеглете решението на проблема
Приложение на общото уравнение на динамиката за изследване на движението на механична система
За механична система определете линейното ускорение a 1 . Да приемем, че масите на блоковете и ролките са разпределени по външния радиус. Кабелите и коланите трябва да се считат за безтегловни и неразтегливи; няма приплъзване. Пренебрегвайте триенето при търкаляне и плъзгане. 
Изтеглете решението на проблема
Приложение на принципа на д'Аламбер за определяне на реакциите на опорите на въртящо се тяло
Вертикалният вал AK, въртящ се равномерно с ъглова скорост ω = 10 s -1, е фиксиран от опорен лагер в точка A и цилиндричен лагер в точка D.
Твърдо закрепени към вала са безтегловен прът 1 с дължина l 1 = 0,3 m, в свободния край на който има товар с маса m 1 = 4 kg, и хомогенен прът 2 с дължина l 2 = 0,6 m, с маса m 2 = 8 kg. И двата пръта лежат в една и съща вертикална равнина. Точките на закрепване на прътите към вала, както и ъглите α и β са посочени в таблицата. Размери AB=BD=DE=EK=b, където b = 0,4 m Вземете товара като материална точка.
Пренебрегвайки масата на вала, определете реакциите на опорния лагер и лагера.

20-то изд. - М.: 2010.- 416 с.
Книгата очертава основите на механиката на материална точка, система от материални точки и твърдо тяло в обем, съответстващ на програмите на техническите университети. Дадени са много примери и задачи, чиито решения са придружени със съответните методически указания. За студенти редовна и задочна форма на технически университети.
формат: pdf
размер: 14 MB
Гледайте, изтеглете: drive.google
СЪДЪРЖАНИЕ
Предговор към тринадесетото издание 3
Въведение 5
РАЗДЕЛ ПЪРВИ СТАТИКА НА ТВЪРДОТО ТЯЛО
Глава I. Основни понятия и начални разпоредби на членове 9
41. Абсолютно твърдо тяло; сила. Статични проблеми 9
12. Първоначални положения на статиката » 11
$ 3. Връзки и техните реакции 15
Глава II. Добавяне на сили. Конвергентна силова система 18
§4. Геометрично! Метод за комбиниране на силите. Резултат от сближаващи се сили, разширение на сили 18
f 5. Проекции на сила върху ос и върху равнина, Аналитичен метод за определяне и добавяне на сили 20
16. Равновесие на система от събиращи се сили_. . . 23
17. Решаване на задачи по статика. 25
Глава III. Силов момент около центъра. Силова двойка 31
i 8. Силов момент спрямо центъра (или точка) 31
| 9. Двойка сили. Момент на двойка 33
f 10*. Теореми за еквивалентност и събиране на двойки 35
Глава IV. Привеждане на системата от сили към центъра. Условия на равновесие... 37
f 11. Теорема за успоредно предаване на сила 37
112. Привеждане на система от сили към даден център - . , 38
§ 13. Условия за равновесие на система от сили. Теорема за момента на резултантната 40
Глава V. Плоска система от сили 41
§ 14. Алгебрични моменти на сила и двойки 41
115. Привеждане плоска системасила до най-простата форма.... 44
§ 16. Равновесие на равнинна система от сили. Случаят на успоредни сили. 46
§ 17. Решаване на задачи 48
118. Равновесие на системи от тела 63
§ 19*. Статично определени и статически неопределени системи от тела (конструкции) 56"
f 20*. Определение за вътрешни усилия. 57
§ 21*. Разпределени сили 58
E22*. Изчисляване на плоски ферми 61
Глава VI. Триене 64
! 23. Закони на триенето при плъзгане 64
: 24. Реакции на груби връзки. Ъгъл на триене 66
: 25. Равновесие при наличие на триене 66
(26*. Триене на нишка върху цилиндрична повърхност 69
1 27*. Триене при търкаляне 71
Глава VII. Пространствена силова система 72
§28. Силов момент около оста. Изчисляване на главен вектор
и главният момент на силовата система 72
§ 29*. Привеждане на пространствената система от сили в нейната най-проста форма 77
§тридесет. Равновесие на произволна пространствена система от сили. Случай на успоредни сили
Глава VIII. Център на тежестта 86
§31. Център на паралелни сили 86
§ 32. Силово поле. Център на тежестта на твърдо тяло 88
§ 33. Координати на центровете на тежестта на еднородни тела 89
§ 34. Методи за определяне на координатите на центровете на тежестта на телата. 90
§ 35. Центрове на тежестта на някои еднородни тела 93
РАЗДЕЛ ВТОРИ КИНЕМАТИКА НА ТОЧКА И ТВЪРДО ТЯЛО
Глава IX. Кинематика на точка 95
§ 36. Въведение в кинематиката 95
§ 37. Методи за уточняване на движението на точка. . 96
§38. Вектор на точковата скорост. 99
§ 39. Вектор на „въртящия момент на точка 100“
§40. Определяне на скоростта и ускорението на точка с помощта на координатния метод за определяне на движение 102
§41. Решаване на задачи по точкова кинематика 103
§ 42. Оси на естествен тристен. Числова стойност на скоростта 107
§ 43. Тангенса и нормално ускорение на точка 108
§44. Някои частни случаи на движение на точка PO
§45. Графики на движение, скорост и ускорение на точка 112
§ 46. Решаване на задачи< 114
§47*. Скорост и ускорение на точка в полярни координати 116
Глава X. Постъпателни и въртеливи движения на твърдо тяло. . 117
§48. Движение напред 117
§ 49. Въртеливо движение на твърдо тяло около ос. Ъглова скорост и ъглово ускорение 119
§50. Равномерно и равномерно въртене 121
§51. Скорости и ускорения на точки на въртящо се тяло 122
Глава XI. Равнопаралелно движение на твърдо тяло 127
§52. Уравнения на равнинно-паралелно движение (движение плоска фигура). Разлагане на движението на транслационно и ротационно 127
§53*. Определяне на траекториите на точки от равнинна фигура 129
§54. Определяне на скоростите на точки на равнинна фигура 130
§ 55. Теорема за проекциите на скоростите на две точки върху тяло 131
§ 56. Определяне на скоростите на точки от плоска фигура с помощта на моментния център на скоростите. Концепцията за центроидите 132
§57. Решаване на проблеми 136
§58*. Определяне на ускоренията на точки от равнинна фигура 140
§59*. Незабавен център за ускорение "*"*
Глава XII*. Движението на твърдо тяло около фиксирана точка и движението на свободно твърдо тяло 147
§ 60. Движение на твърдо тяло с една неподвижна точка. 147
§61. Кинематични уравнения на Ойлер 149
§62. Скорости и ускорения на точките на тялото 150
§ 63. Общ случай на движение на свободно твърдо тяло 153
Глава XIII. Сложно движение на точки 155
§ 64. Относителни, преносими и абсолютни движения 155
§ 65, Теорема за събиране на скорости » 156
§66. Теорема за добавяне на ускорения (теорема на Кориол) 160
§67. Решаване на проблеми 16*
Глава XIV*. Сложно движение на твърдо тяло 169
§68. Добавяне на транслационни движения 169
§69. Събиране на завъртания около две успоредни оси 169
§70. Цилиндрични зъбни колела 172
§ 71. Събиране на завъртания около пресичащи се оси 174
§72. Добавяне на транслационни и ротационни движения. Движение на винта 176
РАЗДЕЛ ТРЕТИ ДИНАМИКА НА ТОЧКА
Глава XV: Въведение в динамиката. Закони на динамиката 180
§ 73. Основни понятия и определения 180
§ 74. Закони на динамиката. Задачи на динамиката на материална точка 181
§ 75. Системи единици 183
§76. Основни видове сили 184
Глава XVI. Диференциални уравнения на движение на точка. Решаване на задачи по динамика на точки 186
§ 77. Диференциални уравнения, движение на материална точка № 6
§ 78. Решение на първата задача от динамиката (определяне на силите от дадено движение) 187
§ 79. Решение на основната задача на динамиката за праволинейно движение на точка 189
§ 80. Примери за решаване на задачи 191
§81*. Падане на тяло в съпротивителна среда (във въздуха) 196
§82. Решение на основната задача на динамиката, с криволинейно движение на точка 197
Глава XVII. Общи теореми на точковата динамика 201
§83. Количеството движение на точка. Силов импулс 201
§ S4. Теорема за промяната на импулса на точка 202
§ 85. Теорема за промяната на ъгловия момент на точка (теорема за моментите) " 204
§86*. Движение под въздействието на централна сила. Закон за областите... 266
§ 8-7. Работа на силата. Мощност 208
§88. Примери за изчислителна работа 210
§89. Теорема за промяната на кинетичната енергия на точка. „... 213J
Глава XVIII. Несвободно и спрямо движението на точка 219
§90. Несвободно движение на точката. 219
§91. Относително движение на точка 223
§ 92. Влиянието на въртенето на Земята върху равновесието и движението на телата... 227
§ 93*. Отклонение на точката на падане от вертикалата поради въртенето на Земята “230
Глава XIX. Праволинейни трептения на точка. . . 232
§ 94. Свободни вибрации без отчитане на съпротивителните сили 232
§ 95. Свободни трептения с вискозно съпротивление (затихващи трептения) 238
§96. Принудителни вибрации. Rezonayas 241
Глава XX*. Движение на тяло в полето на тежестта 250
§ 97. Движение на хвърлено тяло в гравитационното поле на Земята "250
§98. Изкуствени спътници на Земята. Елиптични траектории. 254
§ 99. Концепцията за безтегловност." Местни референтни системи 257
РАЗДЕЛ ЧЕТВЪРТИ ДИНАМИКА НА СИСТЕМАТА И ТВЪРДОТО ТЯЛО
G i a v a XXI. Въведение в системната динамика. Моменти на инерция. 263
§ 100. Механична система. Външни и вътрешни сили 263
§ 101. Маса на системата. Център на масата 264
§ 102. Инерционен момент на тяло спрямо ос. Радиус на инерция. . 265
$ 103. Инерционни моменти на тяло спрямо успоредни оси. Теорема на Хюйгенс 268
§ 104*. Центробежни инерционни моменти. Понятия за главните инерционни оси на тялото 269
$105*. Инерционният момент на тялото спрямо произволна ос. 271
Глава XXII. Теорема за движението на центъра на масата на системата 273
$ 106. Диференциални уравнения на движение на система 273
§ 107. Теорема за движението на центъра на масата 274
$ 108. Закон за запазване на движението на центъра на масата 276
§ 109. Решаване на задачи 277
Глава XXIII. Теорема за изменението на количеството на подвижна система. . 280
$ НО. Количество движение на системата 280
§111. Теорема за промяната на импулса 281
§ 112. Закон за запазване на импулса 282
$113*. Приложение на теоремата към движението на течност (газ) 284
§ 114*. Тяло с променлива маса. Ракетно движение 287
Гдава XXIV. Теорема за промяна на ъгловия момент на система 290
§ 115. Главен момент на импулса на системата 290
$ 116. Теорема за промените в главния момент на количествата на движение на системата (теорема за моментите) 292
$117. Закон за запазване на главния ъглов момент. . 294
$118. Разрешаване на проблеми 295
$119*. Приложение на теоремата за моментите към движението на течност (газ) 298
§ 120. Условия на равновесие за механична система 300
Глава XXV. Теорема за промяната на кинетичната енергия на система. . 301.
§ 121. Кинетична енергия на системата 301
$122. Някои случаи на изчисляване работят 305
$ 123. Теорема за промяната на кинетичната енергия на системата 307
$124. Решаване на задачи 310
$125*. Смесени задачи „314
$126 Потенциално силово поле и силова функция 317
$127, потенциална енергия. Закон за опазване механична енергия 320
Глава XXVI. „Приложение на общите теореми към динамиката на твърдото тяло 323
$12&. Ротационно движение на твърдо тяло около фиксирана ос ". 323"
$129 Физическо махало. Експериментално определяне на инерционните моменти. 326
$130. Равнопаралелно движение на твърдо тяло 328
$131*. Елементарна теория на жироскопа 334
$132*. Движението на твърдо тяло около фиксирана точка и движението на свободно твърдо тяло 340
Глава XXVII. Принцип на Д'Аламбер 344
$ 133. Принципът на Д'Аламбер за точка и механична система. . 344
$134. Основен вектор и Основната точкаинерционни сили 346
$135 Решаване на задачи 348
$136*, Дидемични реакции, действащи върху оста на въртящо се тяло. Балансиране на въртящи се тела 352
Глава XXVIII. Принципът на възможните премествания и общото уравнение на динамиката 357
§ 137. Класификация на връзките 357
§ 138. Възможни движения на системата. Брой степени на свобода. . 358
§ 139. Принципът на възможните движения 360
§ 140. Решаване на задачи 362
§ 141. Общо уравнение на динамиката 367
Глава XXIX. Условия на равновесие и уравнения на движение на система в обобщени координати 369
§ 142. Обобщени координати и обобщени скорости. . . 369
§ 143. Обобщени сили 371
§ 144. Условия за равновесие на система в обобщени координати 375
§ 145. Уравнения на Лагранж 376
§ 146. Решаване на задачи 379
Глава XXX*. Малки колебания на системата около положението на устойчиво равновесие 387
§ 147. Концепцията за устойчивост на равновесие 387
§ 148. Малки свободни трептения на система с една степен на свобода 389
§ 149. Малки затихващи и принудени трептения на система с една степен на свобода 392
§ 150. Малки комбинирани трептения на система с две степени на свобода 394
Глава XXXI. Теория на елементарния удар 396
§ 151. Основно уравнение на теорията на удара 396
§ 152. Общи теореми на теорията на удара 397
§ 153. Коефициент на възстановяване на удара 399
§ 154. Удар на тяло върху неподвижно препятствие 400
§ 155. Пряк централен удар на две тела (удар на топки) 401
§ 156. Загуба на кинетична енергия при нееластичен сблъсък на две тела. Теорема на Карно 403
§ 157*. Удряне на въртящо се тяло. Ударен център 405
Предметен индекс 409
Общи теореми за динамиката на система от тела. Теореми за движението на центъра на масата, за изменението на импулса, за изменението на главния ъглов момент, за изменението на кинетичната енергия. Принципи на Д'Аламбер и възможни движения. Общо уравнение на динамиката. Уравнения на Лагранж.
СъдържаниеРаботата, извършена от силата, е равно на скаларното произведение на векторите на силата и безкрайно малкото преместване на точката на нейното приложение:
,
т.е. произведението на абсолютните стойности на векторите F и ds по косинуса на ъгъла между тях.
Работата, извършена от момента на силата, е равно на скаларното произведение на векторите на въртящия момент и безкрайно малкия ъгъл на въртене:
.
принцип на д'Аламбер
Същността на принципа на д'Аламбер е да сведе проблемите на динамиката до проблеми на статиката. За целта се приема (или е известно предварително), че телата на системата имат определени (ъглови) ускорения. След това се въвеждат инерционни сили и (или) моменти на инерционни сили, които са равни по големина и противоположни по посока на силите и моментите на силите, които според законите на механиката биха създали дадени ускорения или ъглови ускорения
Нека разгледаме един пример. Тялото претърпява постъпателно движение и върху него действат външни сили. Освен това приемаме, че тези сили създават ускорение на центъра на масата на системата. Според теоремата за движението на центъра на масата центърът на масата на тялото би имал същото ускорение, ако върху тялото действа сила. След това въвеждаме силата на инерцията:
.
След това проблемът с динамиката:
.
;
.
За въртеливо движениенаправи същото. Нека тялото се върти около оста z и върху него действат външни моменти на сила M e zk . Приемаме, че тези моменти създават ъглово ускорение ε z. След това въвеждаме момента на инерционните сили M И = - J z ε z. След това проблемът с динамиката:
.
Превръща се в статичен проблем:
;
.
Принципът на възможните движения
Принципът на възможните премествания се използва за решаване на проблеми със статиката. В някои задачи дава по-кратко решение от съставянето на равновесни уравнения. Това важи особено за системи с връзки (например системи от тела, свързани с нишки и блокове), състоящи се от много тела
Принципът на възможните движения.
За равновесието на механична система с идеални връзки е необходимо и достатъчно сумата от елементарните работи на всички действащи върху нея активни сили за всяко възможно движение на системата да е равна на нула.
Възможно преместване на системата- това е малко движение, при което не се прекъсват връзките, наложени на системата.
Идеални връзки- това са връзки, които не извършват работа, когато системата се движи. По-точно количеството работа, извършена от самите връзки при преместване на системата, е нула.
Общо уравнение на динамиката (принцип на Д'Аламбер - Лагранж)
Принципът на Д'Аламберт-Лагранж е комбинация от принципа на Д'Аламберт с принципа на възможните движения. Тоест, когато решаваме динамичен проблем, ние въвеждаме инерционни сили и свеждаме проблема до статичен проблем, който решаваме, използвайки принципа на възможните премествания.
Принцип на Д'Аламбер-Лагранж.
Когато механична система с идеални връзки се движи, във всеки момент сумата от елементарните работи на всички приложени активни сили и всички инерционни сили върху всяко възможно движение на системата е нула:
.
Това уравнение се нарича общо уравнение на динамиката.
Уравнения на Лагранж
Обобщени q координати 1, q 2, ..., q n е набор от n величини, които еднозначно определят позицията на системата.
Броят на обобщените координати n съвпада с броя на степените на свобода на системата.
Обобщени скоростиса производни на обобщени координати по време t.
Обобщени сили Q 1 , Q 2 , ..., Q n
.
Нека разгледаме възможно движение на системата, при което координатата q k ще получи движение δq k. Останалите координати остават непроменени. Нека δA k е работата, извършена от външни сили по време на такова движение. Тогава
δA k = Q k δq k , или
.
Ако при възможно движение на системата всички координати се променят, тогава работата, извършена от външни сили по време на такова движение, има формата:
δA = Q 1 δq 1 + Q 2 δq 2 + ... + Q n δq n.
Тогава обобщените сили са частични производни на работата върху преместванията:
.
За потенциални силис потенциал Π,
.
Уравнения на Лагранжса уравненията на движение на механична система в обобщени координати:
Тук Т е кинетична енергия. Това е функция на обобщени координати, скорости и, вероятно, време. Следователно неговата частна производна също е функция на обобщени координати, скорости и време. След това трябва да вземете предвид, че координатите и скоростите са функции на времето. Следователно, за да намерите общата производна по отношение на времето, трябва да приложите правилото за диференциране на сложна функция:
.
Препратки:
С. М. Тарг, Кратък курстеоретична механика, "Висше училище", 2010г.
В статиката състояние на равновесие се разбира като състояние, при което всички части на механична система са в покой спрямо някаква инерционна координатна система. Един от основните обекти на статиката са силите и техните точки на приложение.
Силата, действаща върху материална точка с радиус-вектор от други точки, е мярка за влиянието на други точки върху разглежданата точка, в резултат на което тя получава ускорение спрямо инерциалната отправна система. величина силаопределя се по формулата:
,
където m е масата на точката – величина, която зависи от свойствата на самата точка. Тази формула се нарича втори закон на Нютон.
Приложение на статиката в динамиката
Важна характеристика на уравненията на движението на абсолютно твърдо тяло е, че силите могат да бъдат преобразувани в еквивалентни системи. С тази трансформация уравненията на движението запазват формата си, но системата от сили, действащи върху тялото, може да се трансформира в по-проста система. Така точката на прилагане на силата може да се премества по линията на нейното действие; силите могат да бъдат разширени според правилото на успоредника; силите, приложени в една точка, могат да бъдат заменени с тяхната геометрична сума.
Пример за такива трансформации е гравитацията. Действа върху всички точки на твърдото тяло. Но законът за движение на тялото няма да се промени, ако силата на гравитацията, разпределена във всички точки, се замени с един вектор, приложен в центъра на масата на тялото.
Оказва се, че ако към основната система от сили, действащи върху тялото, добавим еквивалентна система, в която посоките на силите се променят на противоположни, тогава тялото под въздействието на тези системи ще бъде в равновесие. По този начин задачата за определяне на еквивалентни системи от сили се свежда до проблем за равновесие, тоест до проблем със статиката.
Основната задача на статикатае установяването на закони за трансформиране на система от сили в еквивалентни системи. По този начин методите на статиката се използват не само при изследване на тела в равновесие, но и в динамиката на твърдо тяло, когато се трансформират силите в по-прости еквивалентни системи.
Статика на материална точка
Нека разгледаме материална точка, която е в равновесие. И нека върху него действат n сили, k = 1, 2, ..., н.
Ако една материална точка е в равновесие, тогава векторната сума на силите, действащи върху нея, е равна на нула:
(1)
.
В равновесие геометричната сума на силите, действащи върху дадена точка, е нула.
Геометрична интерпретация. Ако поставите началото на втория вектор в края на първия вектор и поставите началото на третия в края на втория вектор и след това продължите този процес, тогава краят на последния, n-ти вектор ще бъде подравнен с началото на първия вектор. Тоест, получаваме затворена геометрична фигура, дължините на страните са равни на модулите на векторите. Ако всички вектори лежат в една и съща равнина, тогава получаваме затворен многоъгълник.
Често е удобно да избирате правоъгълна координатна система Oxyz. Тогава сумите от проекциите на всички вектори на сила върху координатните оси са равни на нула:
Ако изберете посока, определена от някакъв вектор, тогава сумата от проекциите на векторите на силата върху тази посока е равна на нула:
.
Нека умножим уравнение (1) скаларно по вектора:
.
Ето скаларното произведение на векторите и .
Обърнете внимание, че проекцията на вектора върху посоката на вектора се определя от формулата:
.
Статика на твърдото тяло
Силов момент около точка
Определяне на момент на сила
Момент на сила, приложен към тялото в точка А, спрямо неподвижния център О, се нарича вектор, равен на векторното произведение на векторите и:(2) .
Геометрична интерпретация

Силовият момент е равен на произведението на силата F и рамото OH.
Нека векторите и са разположени в чертожната равнина. Съгласно свойството на векторния продукт, векторът е перпендикулярен на векторите и, тоест, перпендикулярен на равнината на чертежа. Посоката му се определя от правилото за десния винт. На фигурата векторът на въртящия момент е насочен към нас. Абсолютна стойност на въртящия момент:
.
От тогава
(3)
.
Използвайки геометрията, можем да дадем различна интерпретация на момента на силата. За да направите това, начертайте права линия AH през вектора на силата. От центъра O спускаме перпендикуляра OH към тази права линия. Дължината на този перпендикуляр се нарича рамо на силата. Тогава
(4)
.
Тъй като , то формули (3) и (4) са еквивалентни.
По този начин, абсолютна стойност на момента на силатаспрямо центъра O е равно на произведение на сила на рамотази сила спрямо избрания център O.
Когато се изчислява въртящият момент, често е удобно силата да се разложи на два компонента:
,
Където . Силата минава през точка О. Следователно неговият момент е нула. Тогава
.
Абсолютна стойност на въртящия момент:
.
Моментни компоненти в правоъгълна координатна система
Ако изберем правоъгълна координатна система Oxyz с център в точка O, тогава моментът на сила ще има следните компоненти:
(5.1)
;
(5.2)
;
(5.3)
.
Ето координатите на точка А в избраната координатна система:
.
Компонентите представляват съответно стойностите на момента на силата около осите.
Свойства на момента на силата спрямо центъра
Моментът около центъра O, дължащ се на силата, преминаваща през този център, е равен на нула.
Ако точката на прилагане на силата се премести по линия, минаваща през вектора на силата, тогава моментът с такова движение няма да се промени.
Моментът от векторната сума на силите, приложени към една точка на тялото, е равен на векторната сума на моментите от всяка от силите, приложени към същата точка:
.
Същото важи и за сили, чиито продължаващи линии се пресичат в една точка.
Ако векторната сума на силите е нула:
,
тогава сумата от моментите от тези сили не зависи от позицията на центъра, спрямо който се изчисляват моментите:
.
Двойка сили
Двойка сили- това са две равни по абсолютна величина и противоположни посоки сили, приложени към различни точки на тялото.
Една двойка сили се характеризира с момента, в който те създават. Тъй като векторната сума на силите, влизащи в двойката, е нула, моментът, създаден от двойката, не зависи от точката, спрямо която се изчислява моментът. От гледна точка на статичното равновесие естеството на силите, участващи в двойката, няма значение. Няколко сили се използват, за да укажат, че момент на сила с определена стойност действа върху тялото.
Силов момент около дадена ос
Често има случаи, когато не е необходимо да знаем всички компоненти на момента на силата около избрана точка, а трябва да знаем само момента на силата около избрана ос.
Моментът на силата около ос, минаваща през точка O, е проекцията на вектора на момента на силата спрямо точка O върху посоката на оста.
Свойства на момента на силата около оста
Моментът около оста, дължащ се на силата, преминаваща през тази ос, е равен на нула.
Моментът около ос, дължащ се на сила, успоредна на тази ос, е равен на нула.
Изчисляване на момента на силата около ос

Нека сила действа върху тялото в точка А. Нека намерим момента на тази сила спрямо оста O′O′′.
Нека построим правоъгълна координатна система. Нека оста Oz съвпада с O′O′′. От точка А спускаме перпендикуляра OH на O′O′′. През точките O и A прекарваме оста Ox. Начертаваме оста Oy, перпендикулярна на Ox и Oz. Нека разложим силата на компоненти по осите на координатната система:
.
Силата пресича оста O′O′′. Следователно неговият момент е нула. Силата е успоредна на оста O′O′′. Следователно неговият момент също е нула. Използвайки формула (5.3), намираме:
.
Обърнете внимание, че компонентът е насочен тангенциално към окръжността, чийто център е точка O. Посоката на вектора се определя от правилото за десния винт.
Условия за равновесие на твърдо тяло
В равновесие векторната сума на всички сили, действащи върху тялото, е равна на нула, а векторната сума на моментите на тези сили спрямо произволен неподвижен център е равна на нула:
(6.1)
;
(6.2)
.
Подчертаваме, че центърът O, спрямо който се изчисляват моментите на силите, може да бъде избран произволно. Точка О може да принадлежи на тялото или да се намира извън него. Обикновено центърът O се избира, за да направи изчисленията по-лесни.
Условията на равновесие могат да бъдат формулирани по друг начин.
В равновесие сумата от проекциите на силите във всяка посока, зададена от произволен вектор, е равна на нула:
.
Сумата от моментите на силите спрямо произволна ос O′O′′ също е равна на нула:
.
Понякога такива условия се оказват по-удобни. Има случаи, когато чрез избор на оси изчисленията могат да бъдат опростени.
Център на тежестта на тялото
Нека разгледаме една от най-важните сили - гравитацията. Тук силите не се прилагат в определени точки на тялото, а се разпределят непрекъснато в целия му обем. За всяка област на тялото с безкрайно малък обем ΔV, действа силата на гравитацията. Тук ρ е плътността на веществото на тялото и е ускорението на гравитацията.
Нека е масата на безкрайно малка част от тялото. И нека точка A k определя позицията на този участък. Нека намерим количествата, свързани с гравитацията, които са включени в уравненията на равновесието (6).
Нека намерим сумата от силите на гравитацията, образувани от всички части на тялото:
,
къде е телесната маса. По този начин сумата от гравитационните сили на отделните безкрайно малки части на тялото може да бъде заменена с един вектор на гравитационната сила на цялото тяло:
.
Нека намерим сумата от моментите на тежестта по сравнително произволен начин за избрания център O:
.
Тук сме въвели точка C, която се нарича център на тежесттатела. Положението на центъра на тежестта в координатна система с център точка O се определя по формулата:
(7)
.
Така че, когато се определя статичното равновесие, сумата от силите на гравитацията на отделните части на тялото може да бъде заменена с резултантната
,
приложен към центъра на масата на тялото C, чието положение се определя по формула (7).
Позиция на центъра на тежестта за различни геометрични формимогат да бъдат намерени в съответните справочници. Ако тялото има ос или равнина на симетрия, тогава центърът на тежестта е разположен върху тази ос или равнина. По този начин центровете на тежестта на сфера, кръг или кръг са разположени в центровете на кръговете на тези фигури. Центровете на тежестта на правоъгълен паралелепипед, правоъгълник или квадрат също са разположени в техните центрове - в точките на пресичане на диагоналите.

Равномерно (A) и линейно (B) разпределен товар.
Има и случаи, подобни на гравитацията, когато силите не се прилагат в определени точки на тялото, а се разпределят непрекъснато по повърхността или обема му. Такива сили се наричат разпределени силиили .
(Фигура А). Освен това, както в случая с гравитацията, тя може да бъде заменена от резултантна сила с магнитуд, приложена в центъра на тежестта на диаграмата. Тъй като диаграмата на фигура A е правоъгълник, центърът на тежестта на диаграмата е в нейния център - точка C: | AC| = | CB|. (Фигура B). Може да се замени и с резултата. Големината на резултата е равна на площта на диаграмата:.
Точката на приложение е в центъра на тежестта на диаграмата. Центърът на тежестта на триъгълник с височина h се намира на разстояние от основата. Ето защо .
Сили на триене
Триене при плъзгане. Нека тялото е на равна повърхност. И нека е силата, перпендикулярна на повърхността, с която повърхността действа върху тялото (сила на натиск). Тогава силата на триене при плъзгане е успоредна на повърхността и насочена настрани, предотвратявайки движението на тялото. Най-голямата му стойност е:
,
където f е коефициентът на триене. Коефициентът на триене е безразмерна величина.
Триене при търкаляне. Оставете кръгло тяло да се търкаля или може да се търкаля по повърхността. И нека силата на натиск е перпендикулярна на повърхността, от която повърхността действа върху тялото. Тогава върху тялото, в точката на контакт с повърхността, действа момент на сили на триене, предотвратявайки движението на тялото. Най-голямата стойност на момента на триене е равна на:
,
където δ е коефициентът на триене при търкаляне. Има измерението на дължината.
Препратки:
С. М. Тарг, Кратък курс по теоретична механика, “Висше училище”, 2010 г.
Като част от всеки образователен курс изучаването на физика започва с механика. Не от теоретична, не от приложна или изчислителна, а от добрата стара класическа механика. Тази механика се нарича още Нютонова механика. Според легендата един учен се разхождал в градината и видял ябълка да пада и именно това явление го подтикнало да открие закона за всемирното притегляне. Разбира се, законът винаги е съществувал и Нютон му е дал само разбираема за хората форма, но неговата заслуга е безценна. В тази статия няма да описваме законите на Нютоновата механика възможно най-подробно, но ще очертаем основите, основните знания, дефинициите и формулите, които винаги могат да ви помогнат.
Механиката е дял от физиката, наука, която изучава движението на материалните тела и взаимодействията между тях.
Самата дума е от гръцки произход и се превежда като „изкуството за изграждане на машини“. Но преди да построим машини, ние все още сме като Луната, така че нека следваме стъпките на нашите предци и да изучаваме движението на камъни, хвърлени под ъгъл спрямо хоризонта, и ябълки, падащи върху главите ни от височина h.

Защо изучаването на физиката започва с механиката? Тъй като това е напълно естествено, не трябва ли да започнем с термодинамичното равновесие?!
Механиката е една от най-старите науки и исторически изучаването на физиката започва именно с основите на механиката. Поставени в рамките на времето и пространството, хората всъщност не биха могли да започнат с нещо друго, колкото и да им се искаше. Движещите се тела са първото нещо, на което обръщаме внимание.
Какво е движение?
Механичното движение е промяна в положението на телата в пространството едно спрямо друго във времето.
След това определение съвсем естествено стигаме до понятието референтна рамка. Промяна на положението на телата в пространството едно спрямо друго.Ключови думи тук: един спрямо друг . В края на краищата, пътник в кола се движи спрямо човека, който стои отстрани на пътя, с определена скорост и е в покой спрямо съседа си на седалката до него и се движи с друга скорост спрямо пътника в колата, която ги изпреварва.

Ето защо, за да измерваме нормално параметрите на движещи се обекти и да не се объркаме, имаме нужда отправна система - твърдо свързани помежду си отправно тяло, координатна система и часовник. Например, земята се движи около слънцето в хелиоцентрична референтна система. В ежедневието ние извършваме почти всички наши измервания в геоцентрична референтна система, свързана със Земята. Земята е референтно тяло, спрямо което се движат автомобили, самолети, хора и животни.

Механиката като наука има своя задача. Задачата на механиката е да знае положението на тялото в пространството по всяко време. С други думи, механиката изгражда математическо описание на движението и намира връзки между физическите величини, които го характеризират.
За да продължим напред, се нуждаем от концепцията „ материална точка " Казват, че физиката е точна наука, но физиците знаят колко много приближения и предположения трябва да се направят, за да се постигне съгласие относно точно тази точност. Никой никога не е виждал материална точка или е помирисвал идеален газ, но те съществуват! Просто с тях се живее много по-лесно.
Материална точка е тяло, чийто размер и форма могат да бъдат пренебрегнати в контекста на тази задача.
Раздели на класическата механика
Механиката се състои от няколко раздела
- Кинематика
- Динамика
- Статика
Кинематикаот физическа гледна точка изучава как точно се движи едно тяло. С други думи, този раздел се занимава с количествените характеристики на движението. Намерете скорост, път - типични кинематични проблеми
Динамикарешава въпроса защо се движи по този начин. Тоест, той отчита силите, действащи върху тялото.
Статикаизучава равновесието на телата под въздействието на сили, тоест отговаря на въпроса: защо изобщо не пада?
Граници на приложимост на класическата механика
Класическата механика вече не претендира да бъде наука, която обяснява всичко (в началото на миналия век всичко беше съвсем различно) и има ясна рамка на приложимост. Като цяло законите на класическата механика са валидни в света, с който сме свикнали по размери (макросвят). Те спират да работят в случая със света на частиците, когато квантовата механика замени класическата механика. Също така класическата механика не е приложима в случаите, когато движението на телата се извършва със скорост, близка до скоростта на светлината. В такива случаи релативистките ефекти стават ясно изразени. Грубо казано, в рамките на квантовата и релативистката механика класическата механика е специален случай, когато размерът на тялото е голям и скоростта е ниска.

Най-общо казано, квантовите и релативистичните ефекти никога не изчезват; те се появяват и при обикновеното движение на макроскопични тела със скорост, много по-ниска от скоростта на светлината. Друго нещо е, че ефектът от тези ефекти е толкова малък, че не надхвърля най-точните измервания. По този начин класическата механика никога няма да загуби фундаменталното си значение.
Ще продължим да изучаваме физическите основи на механиката в бъдещи статии. За по-добро разбиране на механиката винаги можете да се обърнете към на нашите автори, които индивидуално ще хвърлят светлина върху тъмното петно на най-трудната задача.
 Тълкуване на сънища сънувал лайна
Тълкуване на сънища сънувал лайна Как да изцедите лимон: съвети и методи. Как да изстискате сок от лимон у дома
Как да изцедите лимон: съвети и методи. Как да изстискате сок от лимон у дома Представители и характеристика на разред насекомоядни
Представители и характеристика на разред насекомоядни DOA на коленните стави: етапи, симптоми и лечение
DOA на коленните стави: етапи, симптоми и лечение Димексид - подробно описание и използване на димексид у дома, ако влезе в стомаха
Димексид - подробно описание и използване на димексид у дома, ако влезе в стомаха Андрей Стигар: Как да направим инвентара печеливш?
Андрей Стигар: Как да направим инвентара печеливш?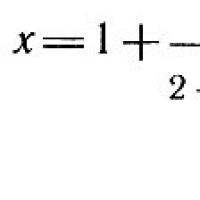 Значение на непрекъснати дроби в речника на Collier
Значение на непрекъснати дроби в речника на Collier